Two-Sided vs One-Sided Hypothesis Tests: A Cautionary Tale
Hypothesis testing is a fundamental concept in statistics used to make decisions about populations based on sample data. When conducting hypothesis tests, researchers often have two options: one-sided and two-sided tests. In this blog, we’ll explore the differences between these two approaches and discuss why one-sided hypothesis tests should be used with caution, if at all.
Let’s say that we are interested in whether the mean IQ of a country is 100. However, we do not observe the IQ of each individual of this country, but we observe only a random sample of about 500 people whose IQ we measured. We can then use hypothesis tests to determine whether the country IQ is 100 based on our random sample of 500 people.
Let’s first assume that we have no prior knowledge or a theory about the IQ of this country, and we are agnostic about whether the IQ is 100, or below 100, or above 100. We have no expectations and we simply do not know what the average IQ is, but we heard it is 100, so we want to test this. For this purpose, we can use a two-sided hypothesis test. A two-sided hypothesis test, also called a two-tailed test, examines whether a population parameter is different from a specific value in either direction. These tests are used when researchers want to determine if there is a significant difference from a hypothesized value, regardless of the direction. We can then formulate two hypotheses, a null hypothesis that the mean IQ is indeed 100 and an alternative hypothesis that the mean IQ is not 100. We can denote this as:
H0 : μ = 100
Ha : μ ≠ 100
With representing the mean IQ of the country.
Now let’s say that we have a theory that the average IQ of this country is actually bigger than 100, for instance because the country is a big IT-hub, attracting highly able people from other countries. For this purpose, we can use a right one-sided hypothesis test. A right one-sided hypothesis test, also known as a right one-tailed test, is designed to test whether a population parameter is greater than a specific value, but not smaller than this value. We can denote this as:
H0 : μ = 100
Ha : μ > 100
Conversely, let’s say that we have a theory that the average IQ of this country is actually smaller than 100, for instance because of the so-called brain drain. Due to poor life circumstances, highly able people have emigrated to another country. For this purpose, we can use a left one-sided hypothesis test. A left one-sided hypothesis test, also known as a left one-tailed test, is designed to test whether a population parameter is smaller than a specific value, but not greater than this value. We can denote this as:
H0 : μ = 100
Ha : μ < 100
Suppose we are using a Z-test (but the same argument applies to most tests e.g., a t-test or a 𝑋2 – test) at a significance level of 5%, so α = 0.05. We can plot the standard normal distribution of the decision to reject the null hypothesis using a two-sided hypothesis test as follows:

We will reject the null hypothesis if the Z-value that we calculated based on our sample (for the calculation of this Z-value, and for an explanation on the plots, take a look at our course on Hypothesis Testing) is greater than or equal to 1.96 or smaller than or equal -1.96.
Now, let’s plot the standard normal distribution of the decision to reject the null hypothesis using a right one-sided hypothesis test:
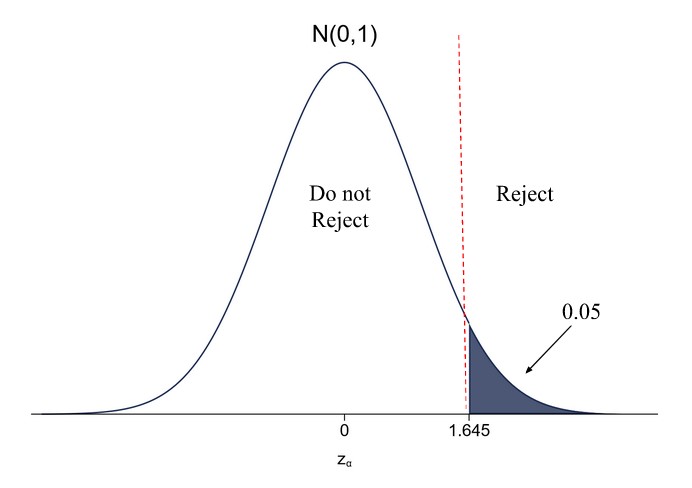
Now, we will reject the null hypothesis if the Z-value that we calculated based on our sample is greater than or equal to 1.645. Similarly, we can plot the standard normal distribution of the decision to reject the null hypothesis using a left one-sided hypothesis test:
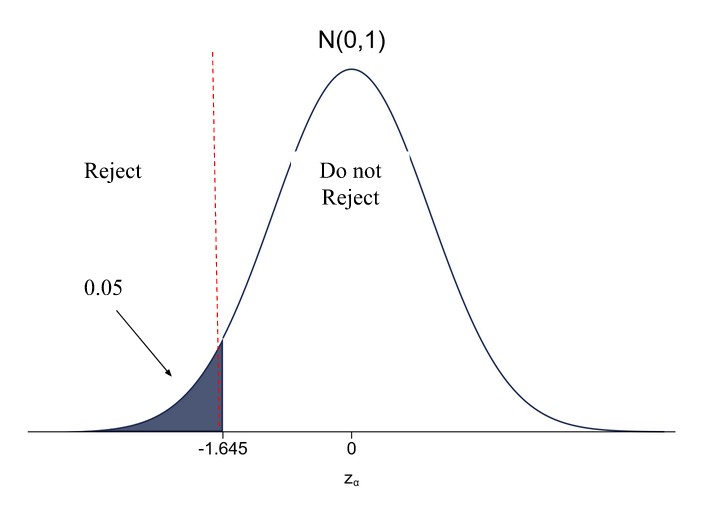
Thus, it is easier to reject the null hypothesis on the side that was hypothesized in the alternative hypothesis when using a one-sided test than when using a two-sided test. For instance, if we hypothesized that the mean IQ of the country was greater than 100, then we would reject the null hypothesis that the IQ is 100 if the Z-value is greater than 1.645 using a right one-sided test, whereas we would reject the null hypothesis if the Z-value is greater than 1.96 using a two-sided test. Clearly, it is easier to reject the null hypothesis using a one-sided test on this side. Hence, we say that compared to the two-sided test, a one-sided test has greater statistical power on this side. However, the downside of this greater statistical power is that we have given up any ability to detect a statistically significant difference on the other side. Thus, if the true mean IQ is lower than 100, we will not be able to detect that using a right one-sided test. Said otherwise, if the true mean IQ is lower than 100, we will be led to believe that the true mean IQ is likely 100 as we failed to reject the null hypothesis (although keep in mind that failing to reject a null hypothesis does not mean you accept it).
In sum, when we choose for a one-sided hypothesis test, we gain statistical power in the direction of the alternative hypothesis, but we lose the ability to detect a significant difference in the other direction.
Knowing this, it may be tempting to first estimate the data, check the direction of the coefficient, and then determine the alternative hypothesis so you can use a one-sided test with higher power and your results have a higher probability to be statistically significant. The same happens when we use p-values. If we choose the alternative hypothesis based on the direction observed in the sample, then the reported p-value will be half of what it should be, and the results are more likely to be significant. This, however, is very poor statistical practice (referred to as p-hacking). Namely, we will be committing a type-I error: we will reject the null hypothesis even though it is true. This also highlights how crucial it is to first have a theory to guide the hypotheses. This way, theory determines the hypotheses (either one-sided or two-sided) and then data is investigated so the researcher is less likely to manipulate the results. In any case, you should never use the data to determine what the alternative hypothesis should be, but hypotheses should flow from a theoretical framework.
Given that unexpected results may occur e.g., expecting that the mean IQ is greater than 100 whereas it is actually lower than 100, most researchers give up the higher power of a one-sided test and opt for a two-sided test. This way, differences in both directions can be detected, and we leave room for unexpected results, which are often the most interesting results. Besides, when using two-tailed tests, we are mostly interested in the direction of the differences anyway, and not just whether a difference exists. For instance, if we investigate whether school closures during the COVID-19 pandemic impacted mental health of children, we are not only interested in whether the school closures had an impact, but also whether school closures decreased (e.g., due to loneliness) or increased (e.g., due to less bullying) mental health.
In the end, the current practice is to report the two-sided p-value, and then let the readers make up their own mind. If a researcher feels that a one-sided test was more appropriate, this researcher can make the adjustment by dividing the p-value by 2 if the direction of the coefficient corresponds to the hypothesized direction. The one-sided p-value in the opposite direction would then be 1-(p-value/2).

Master the Science of Causal Inference
Latest Statistics Insights

Demystifying Degrees of Freedom
Demystifying Degrees of Freedom When doing hypothesis testing, everyone has encountered tests that depend on the so-called ‘degrees of freedom’. However, explanations of what degrees of freedom actually mean are lacking from most textbooks, and if they exist, these explanations are highly formulaic and lack intuition. Indeed, the phrase ‘degrees

Assumptions Under Which The OLS Estimators are BLUE
Assumptions Under Which The OLS Estimators are BLUE An Ordinary Least Squares (OLS) linear regression is one of the most common and widely used techniques in empirical research. In a nutshell, an OLS linear regression relates an outcome Y to a independent variable X by minimizing the sum of squared